Tem umas funções no R que são difíceis de entender como elas funcionam, mas quando se descobre ai você não para mais de usar.
Bem, esse é o meu caso com a função filter.
filter hoje em computação me remete mais a transformação, algo como map do que um filtro estocástico, como é o caso da função filter.
Não vou aqui ficar explicando o que é um filtro estocástico, até porque eu não sei nada sobre isso.
Sei apenas entra um sinal de um lado e do outro sai um ruído branco, ou seja, o sinal é filtrado.
Uma propriedade interessante destes filtros é a reversibilidade, isto é, estes filtros são reversíveis de forma que se você devolve o ruído o sinal aparece do outro lado.
O estudo destes filtros deu origem a família de modelos ARMA (autoregressivos e de médias móveis) e são exatamente os processos estocásticos dessa família que é possível reproduzir com a função filter.
Vou aqui mostrar como gerar os processos autoregressivos (AR) e médias móveis de diferentes ordens e tipos.
Segue a assinatura da função filter.
function (x, filter, method = c("convolution", "recursive"), sides = 2L, circular = FALSE, init = NULL)
Em um primeiro olhar tudo isso parece meio confuso, e de fato é, pessoalmente quebraria essa função e duas, mas esse é um dos pontos negativos do R, o design de diversas funções, principalmente as mais antigas não é muito intuitivo para usuários nos dias atuais, acho que o mesmo acontece com PHP.
Processos Autoregressivos
Para gerar processos autoregressivos considere a seguinte assinatura de filter:
function (x, filter, method="recursive", init=NULL)
onde x é um vetor com o sinal a ser incrementado a cada passo, o argumento filter é um vetor com os coeficientes do filtro, method é "recursive" e init é o estado inicial do processo.
Considerando o sinal de entrada $x_t$ e os coeficientes $\phi_i$ (onde $i = 1,\dots, n$) do filtro, a saída é dada por
$$ y_t = \sum_{i=1}^n \phi_1 y_{t-i} + x_t $$
Dessa forma filter=c(phi_1, ..., phi_n), x=x_t e init deve ser um vetor de mesmo comprimento de filter pois se considerarmos o estado inicial de $y_t$ temos $n$ termos autoregressivos que devem ser definidos para darmos início a recursão.
A equação acima define a estrutura de entradas da função filter de forma que se for possível representar um processo neste formato, é possível utilizar a função filter para reproduzir o processo.
Processo AR(1) — Autoregressivo de primeira ordem
Tipicamente um processo AR(1) é definido como:
$$ y_t = \phi_0 + \phi_1 y_{t-1} + x_t $$
onde $y_t$ é dito autoregressivo por utilizar o seu estado passado, $y_{t-1}$, para descrever o seu estado corrente, $y_t$. Os coeficientes $\phi_0$ e $\phi_1$ são coeficientes do processo, o estado inicial $y_0$ deve ser definido, assim como o sinal $x_t$.
Para utilizar a função filter para gerar um AR(1) vamos reescrever o processo de outra forma
$$ \begin{align} y_t & = \phi_1 y_{t-1} + (\phi_0 + x_t) \\ & = \phi_1 y_{t-1} + x^{\prime}_t \end{align} $$
Dessa forma o termo autoregressivo é aplicado ao coeficiente $\phi_1$.
A chamada a filter fica:
ar1 <- stats::filter(phi_0 + x_t, filter=phi_1, method='recursive', init=y_0)
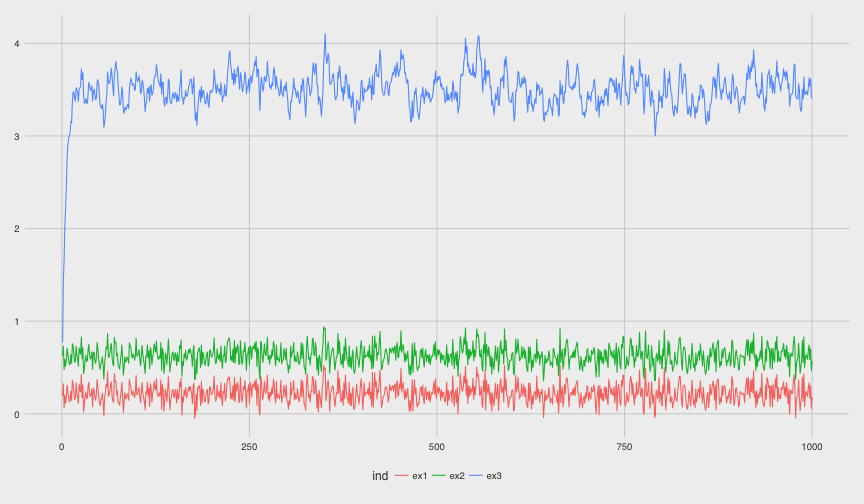
Vamos gerar alguns processos e visualizar os dados:
x_t <- rnorm(1000)*0.1
ar <- stack(list(
ex1=as.numeric(stats::filter(0.2 + x_t, 0.1, method="recursive", init=0)),
ex2=as.numeric(stats::filter(0.5 + x_t, 0.2, method="recursive", init=0.7)),
ex3=as.numeric(stats::filter(0.7 + x_t, 0.8, method="recursive", init=0.1))
))
library(ggplot2)
ggplot(ar, aes(x=rep(1:1000, 3), y=values, colour=ind)) + geom_line()
Médias Móveis
Para calcular a média móvel de uma série temporal considere a seguinte assinatura de filter:
function (x, filter, method="convolution", sides=2L, circular=FALSE)
onde, assim como no caso autoregressivo x é um vetor com o sinal a ser incrementado a cada passo e o argumento filter é um vetor com os coeficientes da média móvel e este argumento determina a quantidade de elementos da média móvel.
method é "convolution", sides refere-se ao modo como a janela móvel do cálculo da média está posicionada, sides=1L para médias móveis apenas com valores passados e sides=2L para médias móveis com janela centrada.
O argumento circular torna o sinal x circular de forma que a média móvel dos instantes iniciais utiliza elementos dos instantes finais.
Abaixo listo alguns exemplos do posicionamento da janela móvel em relação com a definição dos parâmetros side e circular.
Exemplo 1: sides=1 média móvel com janela de 5 elementos calculada em $x_9$
$$ x_0, x_1, x_2, x_3, x_4, \underbrace{x_5, x_6, x_7, x_8, x_9}_{\texttt{sides=1}} $$
Exemplo 2: sides=2 média móvel com janela de 5 elementos centrada calculada em $x_7$
$$ x_0, x_1, x_2, x_3, x_4, \underbrace{x_5, x_6, x_7, x_8, x_9}_{\texttt{sides=2}} $$
Exemplo 3: sides=1, circular=TRUE média móvel circular com janela de 5 elementos calculada em $x_2$
$$ \underbrace{x_8, x_9, x_0, x_1, x_2}_{\texttt{sides=1,circular=T}}, x_3, x_4, x_5, x_6, x_7, x_8, x_9 $$
Exemplo 4: sides=2, circular=TRUE média móvel circular com janela de 5 elementos centrada calculada em $x_9$
$$ x_8, x_9, x_0, x_1, x_2, x_3, x_4, x_5, x_6, \underbrace{x_7, x_8, x_9, x_0, x_1}_{\texttt{sides=2,circular=T}} $$
Média Móvel Simples
A média móvel simples, ou aritmética, é muito usada análise técnica de séries de preço. Vou apresentar um exemplo uma média móvel simples para a série de preços da PETR4. Abaixo segue a preparação dos dados, eu utilizo os preços de fechamento da PETR4, ordeno por data e seleciono apenas o ano de 2012.
library(dplyr)
library(lubridate)
ds <- read.table('datasets/PETR4.daily.raw.csv', sep=',', header=TRUE, stringsAsFactors=F) %>%
mutate(Date=as.Date(Date)) %>%
select(Date, Close) %>%
arrange(Date) %>%
filter(year(Date) == 2012)
Utilizo os dados de fechamento como o sinal para o cálculo da média móvel com a função filter.
Como eu importei o pacote dplyr que também tem uma função filter, eu preciso fazer uma referência ao pacote stats para evitar o conflito de nomes de funções, por isso faço a chamada a stats::filter.
ma <- stats::filter(ds$Close, filter=rep(1/21, 21), method="convolution", sides=1, circular=F)
Calculei uma média móvel simples de 21 dias (equivalente a um mês em dias úteis) com sides=1 e circular=F .
Abaixo organizo os dados da série de preços e da média móvel para apresentar em um gráfico do ggplot.
ds.ma <- stack(list(
Close=ds$Close,
MA=as.numeric(ma)
))
ds.ma$Date <- ds$Date
ggplot(ds.ma, aes(x=Date, y=values, colour=ind)) + geom_line() + theme_light()
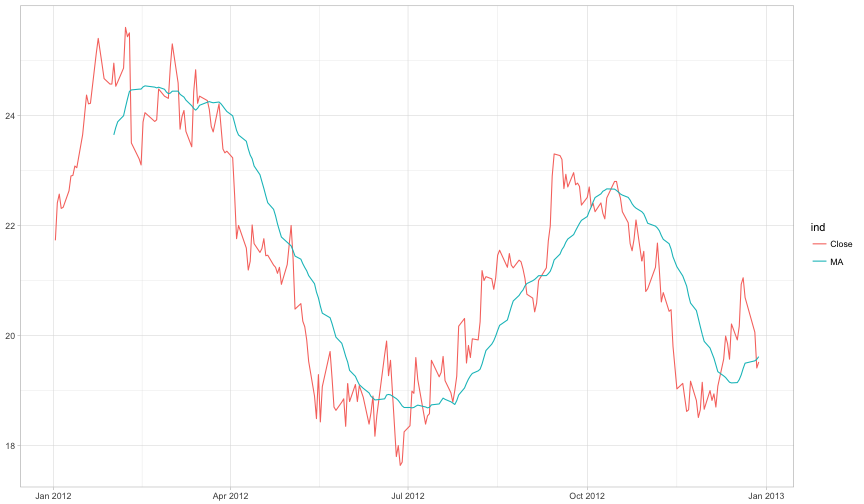
Note que há um deslocamento da média móvel causado pela definição de circular=F, pois a série de preços não é estacionária, não faz sentido utilizar circular.
Entretanto, para a série de retornos já seria uma possibilidade.
Exemplos de processos com filter
Processo AR(2)
Definição:
$$ \begin{align} y_t & = \phi_0 + \phi_1 y_{t-1} + \phi_2 y_{t-2} + x_t \\ & = \phi_1 y_{t-1} + \phi_2 y_{t-2} + \phi_0 + x_t \\ & = \phi_1 y_{t-1} + \phi_2 y_{t-2} + x^\prime_t \\ \end{align} $$
Código:
filter(phi_0 + x_t, filter=c(phi_1, phi_2), method='recursive', init=c(y_0, y_m1))
onde y_m1= $y_{-1}$
Média Móvel Exponencial (EWMA)
Definição:
$$ \begin{align} y_t & = \phi y_{t-1} + (1 - \phi)x_t \\ & = \phi y_{t-1} + x^\prime_t \end{align} $$
onde $0 < \phi < 1$.
Código:
filter((1 - phi)*x_t, filter=phi, method='recursive', init=y_0)
Média Móvel Simples com 3 elementos
Definição:
$$ y_t = \phi_1 x_t + \phi_2 x_{t-1} + \phi_3 x_{t-2} $$
Código:
filter(x, filter=c(phi_1, phi_2, phi_3), method="convolution", sides=1L, circular=FALSE)
Média Móvel centrada com 3 elementos
Definição:
$$ y_t = \phi_1 x_{t+1} + \phi_2 x_{t} + \phi_3 x_{t-1} $$
Código:
filter(x, filter=c(phi_1, phi_2, phi_3), method="convolution", sides=2L, circular=FALSE)
Processo MA(1)
Definição:
$$ \begin{align} y_t & = x_t - \theta x_{t-1} \\ & = \phi_1 x_t + \phi_2 x_{t-1} \end{align} $$
onde $\phi_1 = 1$ e $\phi_2 = -\theta$
Código:
filter(x, filter=c(1, -theta), method="convolution", sides=1L, circular=FALSE)
Processo MA(2)
Definição:
$$ \begin{align} y_t & = x_t - \theta_1 x_{t-1} - \theta_2 x_{t-2} \\ & = \phi_1 x_t + \phi_2 x_{t-1} + \phi_3 x_{t-2} \end{align} $$
onde $\phi_1 = 1$, $\phi_2 = -\theta_1$ e $\phi_3 = -\theta_2$
Código:
filter(x, filter=c(1, -theta_1, -theta_2), method="convolution", sides=1L, circular=FALSE)