Este post é para quem, assim como eu, sempre quis saber de onde vem o coeficiente $\lambda=0.94$ proposto pelo JP Morgan para estimar a volatilidade via EWMA (Exponential Weighted Moving Average).
Vou mostrar aqui como estimar o $\lambda$ utilizando:
- minimização da soma do erro quadrático $S$
- máxima verosimilhança
Ambas abordagens apresentam resultados semelhantes e vamos observar isso claramente nas funções objetivo utilizadas nos processos de otimização. Conhecendo estas técnicas você poderá estimar o coeficiente para qualquer série e assim ter autonomia sobre os resultados produzidos por você.
Dados utilizados
Vou utilizar a série de retornos BOVESPA de março/1997 até março/2014 (retornos contínuos).
bvsp <- read.csv('http://www.quandl.com/api/v1/datasets/YAHOO/INDEX_BVSP.csv?&trim_start=1997-03-12&trim_end=2014-03-31&sort_order=desc', colClasses=c('Date'='Date'))
bvsp.ts <- with(bvsp, as.xts(Close, order.by=as.Date(Date)))
bvsp.r <- diff(log(bvsp.ts))
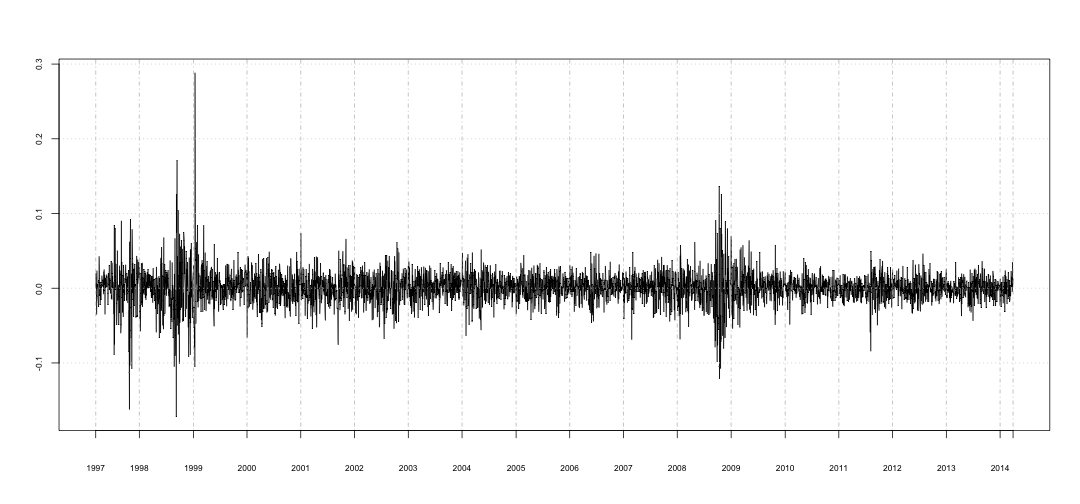
É interessante observar os clusters de volatilidade, os de 1998 e 2008 são os mais relevantes (e curiosamente ocorreram em 10 anos). Clusters menores podem ser observados em 1997 e 2011.
Introduzindo o EWMA
Uma excelente fonte sobre Alisamento Exponencial é Capítulo 4 do livro do Morettin sobre séries temporais. Também sugiro fortemente a leitura do capítulo sobre volatilidade e correlação do livro do Hull. Aqui eu apenas apresentarei a equação que vou utilizar nas próximas seções para estimar o $\lambda$.
O EWMA é definido como:
$$ \sigma^2_n = \lambda\sigma^2_{n-1} + (1-\lambda)r^2_{n-1} $$
onde $\sigma^2_n$ é a variância estimada e $r^2_n$ é o retorno, ambos referentes ao instante $n$.
Abaixo segue uma implemetação do EWMA utilizando closures:
ewma_builder <- function(rets, init=c('zero', 'first', 'var')) {
.check_init <- function(value) (init == value)[1]
.rets <- na.trim(rets)
.n <- length(.rets)
if (.check_init('zero')) {
.init <- 0
} else if (.check_init('first')) {
.init <- as.numeric(.rets[1]^2)
} else if (.check_init('var')) {
.init <- as.numeric(var(.rets))
} else if (is.numeric(init)) {
.init <- as.numeric(init)
} else {
stop('unknown init: ', init)
}
.r2 <- .rets^2
function(lambda) {
r2 <- (1 - lambda)*.r2
s <- filter(r2, lambda, "recursive", init=.init)[-.n]
x <- as.xts(s, order.by=index(r2)[-1])
names(x) <- 'EWMA'
x
}
}
A função ewma_builder retorna uma closure que calcula o EWMA para a série de retornos fornecida em rets e considerando $\sigma^2_1$ de acordo com init.
init pode assumir 4 valores:
zeroonde $\sigma^2_1 = 0$firstonde $\sigma^2_1 = r^2_1$varonde $\sigma^2_1$ é a variância amostral- um número para ser utilizado diretamente como $\sigma_1^2$
Pontos importantes:
- A função retornada calcula a variância na frequência da série de retornos fornecida, portanto, uma série diária retornará variância diária e para obter a volatilidade anualizada é necessário $\sqrt{252 \cdot}$.
- $\sigma^2_1$ não é retornado pela função que calcula a variância. Entendo que $\sigma^2_1$ é uma suposição que contribui para a convergência das estimativas de volatilidade, portanto, não incluo esse chute na série retornada.
- A função
ewma_builderfoi desenvolvida para receber sériesxtsouzoo.
Abaixo segue o cálculo da volatilidade utilizando $\lambda=0.94$.
compute_ewma <- ewma_builder(bvsp.r, 'first')
x.ewma <- sqrt(compute_ewma(0.94))
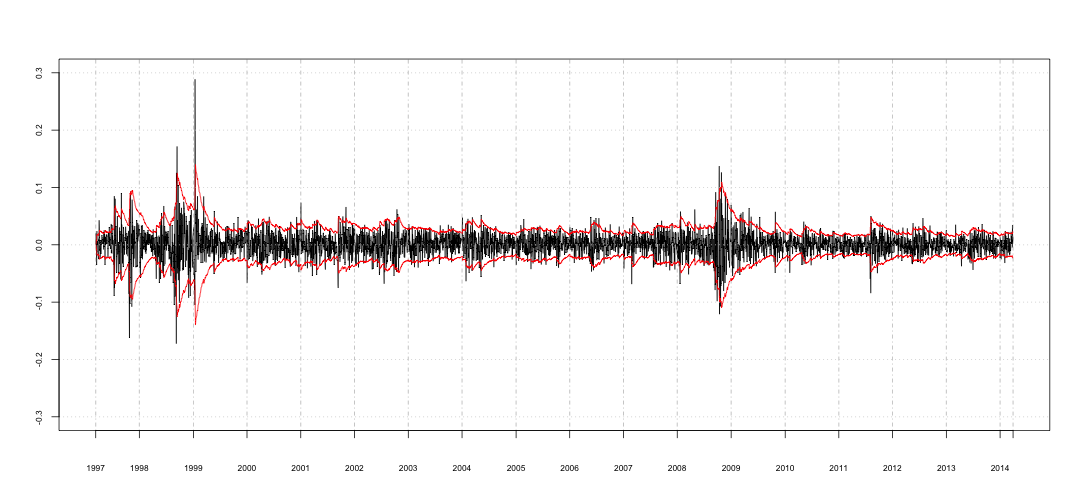
Note que considero $\sigma^2_1=r^2_1$.
Estimando via minimização de $S$
$S$ é a soma do erro quadrático, ou seja:
$$ S = \sum^N_{n=1}(s^2_n - \sigma^2_n)^2 $$
é a soma quadrado da diferença entre a variância estimada $\sigma^2_n$ e a variância observada $s^2_n$, para uma amostra de tamanho $N$. O $\lambda$ que nos interessa é aquele que minimiza essa soma.
Aqui temos o primeiro obstáculo:
quem é $s^2$?
Antes de definir a variância observada (o que chega a ser um contrasenso dado que não observamos a variância de fato) vou listar duas alternativas:
- retorno quadrático $r^2_n$: é uma alternativa honesta pois assim estariamos utilizando EWMA para estimar o retorno quadrático 1 passo a frente.
- desvio padrão amostral dos próximos $T$ pontos: uma alternativa mais ambiciosa tentando prever uma janela maior no futuro. Segundo Hull essa foi a abordagem adotada pelo JPMorgan para chegar ao $\lambda=0.94$, eles utilizaram $T=25$.
Nas próximas sessões vou encontrar $\lambda$ em ambas as abordagens.
Utilizando o retorno quadrático
Para encontrar $\lambda$ minimizando $S$ e considerando o retorno quadrático como variância observada
$$ S = \sum^N_{n=1} (r^2_n - \sigma^2_n) $$
precisamos construir a função objetivo que retorne $S$ para uma dado $\lambda$. A função abaixo retorna uma closure que faz isso.
f_obj_builder <- function(rets, init='first') {
.mean <- mean(rets, na.rm=TRUE)
.rets <- rets - .mean
compute_ewma <- ewma_builder(.rets, init)
.r2 <- .rets^2
function(lambda) {
.ewma <- compute_ewma(lambda)
sum(na.omit((.r2 - .ewma)^2))
}
}
Note que tiro diretamente a diferença entre o retorno quadrático e .ewma, pois dado que ambos são séries temporais xts, tenho a garantida de que as operações serão realizadas entre elementos da mesma data.
Para encontrar $\lambda$ basta minimizar a função objetivo.
Vou utilizar a função optimize.
Essa função procura o menor valor em um intervalo dado para uma função com apenas 1 parâmetro.
Como a nossa função objetivo recebe apenas $\lambda$ e sabemos que $0 < \lambda < 1$, optimize resolve o nosso problema.
f_obj <- f_obj_builder(bvsp.r, 'first')
(o <- optimize(f_obj, c(0, 1)))
## $minimum
## [1] 0.9091
##
## $objective
## [1] 0.01267
O valor encontrado foi $\lambda = 0.91$ e não fica muito longe do $0.94$ proposto pelo RiskMetrics.
Uma coisa interessante é olhar o comportamento da função objetivo. Dado que temos a função objetivo e ela tem apenas 1 argumento, fica fácil vê-la em um gráfico:
s <- seq(0.5, 1, length.out=1000)
t <- sapply(s, f_obj)
plot(s, t, type='l', xlim=c(0.5, 1))
abline(h=o$objective, col='red')

Olhando o gráfico observamos que há apenas 1 ponto de mínimo na função e que este está bem próximo a $\lambda = 0.91$.
Podemos agora calcular a variância da série e visualizar o resultado.
x.ewma <- compute_ewma(0.91)
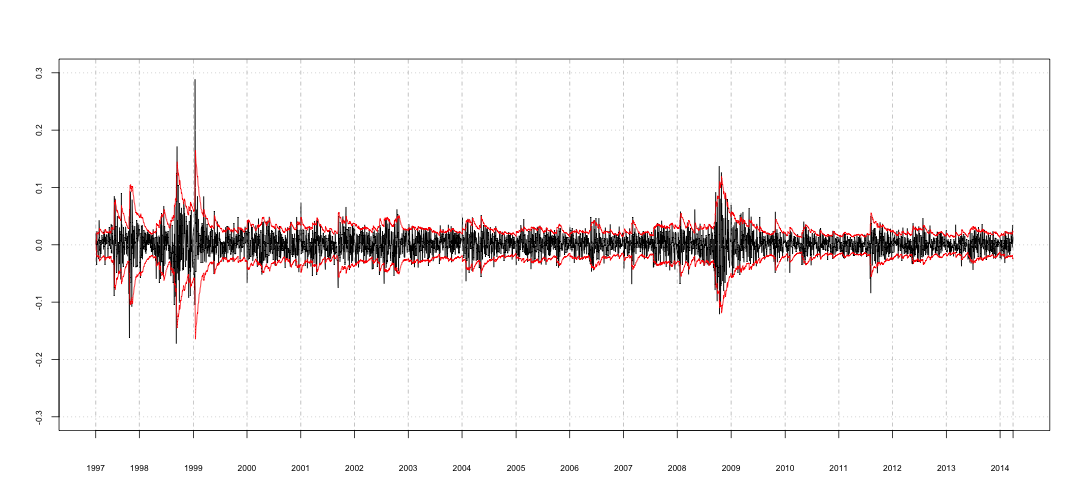
Utilizando o desvio padrão futuro
Agora para encontrar $\lambda$ minimizando $S$ e considerando que o desvio padrão dos próximos $T$ pontos, $v_n$, é a variância observada.
$$ S = \sum^N_{n=1} (v_n - \sigma^2_n) $$
precisamos construir a seguinte função objetivo.
f_obj_builder <- function(rets, width, init='first') {
.mean <- mean(rets, na.rm=TRUE)
.rets <- rets - .mean
.var <- rollapply(.rets, var, width=width, align='left')
compute_ewma <- ewma_builder(rets, init)
function(lambda) {
.ewma <- compute_ewma(lambda)
sum(na.omit((.var - .ewma)^2))
}
}
Note que essa função recebe, no parâmetro width, a quantidade de pontos que será utilizada no cálculo da variância amostral.
Vou utilizar 25, seguindo a sugestão descrita no Hull.
f_obj <- f_obj_builder(bvsp.r, 25, 'first')
(o <- optimize(f_obj, c(0, 1)))
## $minimum
## [1] 0.9813
##
## $objective
## [1] 0.001958
Desta vez o valor encontrado foi $\lambda = 0.98$, significativamente diferente de $0.91$.
s <- seq(0.5, 1, length.out=1000)
t <- sapply(s, f_obj)
plot(s, t, type='l', xlim=c(0.5, 1))
abline(h=o$objective, col='red')

A função objetivo para esta abordagem também apresenta apenas 1 ponto de mínimo, garantindo a coerência do resultado encontrado.
Vamos novamente ver o gráfico dos retornos envolvidos pela volatilidade para ter uma idéia de como se comporta a volatilidade com relação aos retornos observados utilizando-se um $\lambda$ tão alto.
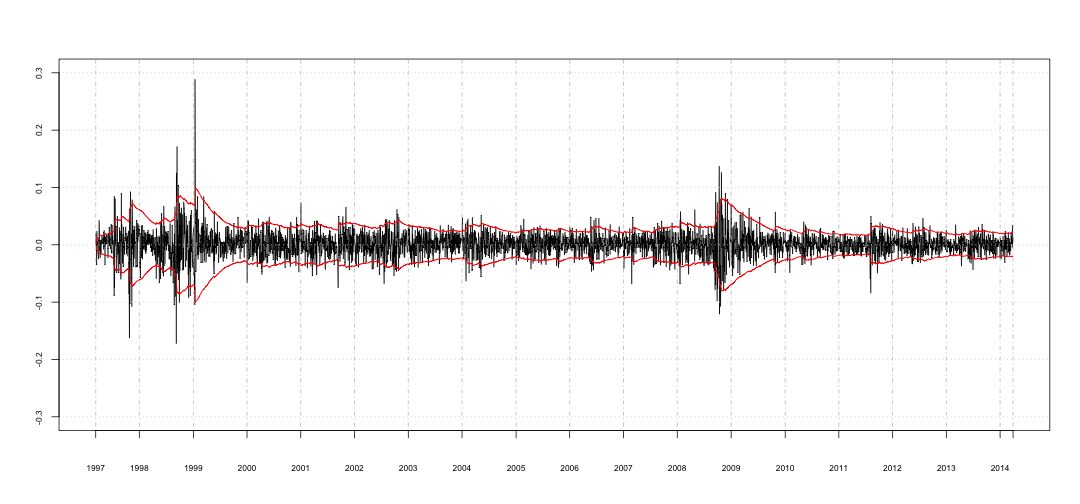
Conclusão
Dada a diferença entre os valores de $\lambda$ é necessária uma reflexão mais profunda sobre o tema. Obviamente a diferença reflete a escolha de $s^2$ e essa deve refletir o objetivo do modelo. Na minha opinião, a primeira abordadem tem como objetivo o forecast da variância de retornos diários, e portanto é mais adequada para o cálculo de VAR diário, por exemplo. Observando a série de retornos identificamos os clusters de volatilidade, que indicam uma mudança de regime da série, o que me leva a supor que o parâmetro $\lambda$ varia ao longo do tempo. Um teste fora da amostra pode ser utilizado para avaliar o período de aderência do modelo encontrado, pois, uma vez que ocorra mudança de regime na série é importante reestimar o parâmetro. O problema aqui torna-se como identificar a mudança de regime.
A segunda abordadem, que apresenta um $\lambda$ alto, na minha opinião, já visa um comportamento mais estacionário. Também pode ser utilizado para calcular o VAR diário, por exemplo, no entanto, poderia ser utilizado para o VAR de janelas maiores como 10 dias, sem perda de generalidade. Acredito que com essa abordagem, a necessidade de reestimar o parâmetro seja menor, dado o efeito da utilização da média na estimação.
Contudo, seria prudente buscar formas quantitativas de comparar as abordagens. Acredito que testes de frequência e testes fora da amostra são boas alternativas.
A estimação via máxima verosimilhança fica para outro post, onde teremos uma técnica que considera premissas relacionadas aos retornos ao invés da variância e assim poderemos ver de qual abordadem ela se aproxima, em termos do $\lambda$ estimado.