getReturns.rÉ necessário carregar o módulo getReturns.r que contém a função getReturnsFromYahooFiles, que será útil para gerar os retornos a partir dos dados baixados do Yahoo! Finance.
source("scripts/getReturns.r")
Os arquivos CSV foram baixados do Yahoo! Finance e contém os dados de preços das ações com periodicidade mensal (referentes ao começo de cada mês).
A função getReturnsFromYahooFiles carrega os arquivos e devolve as séries de retornos referentes a coluna de preço de fechamento ajustado (Adj.Close).
filelist <- c("data/VALE3.monthly.raw.csv", "data/PETR3.monthly.raw.csv")
returns.monthly.x <- getReturnsFromYahooFiles(filelist)
## VALE3 PETR3
## Feb 2000 0.01646 0.234749
## Mar 2000 -0.01646 0.024317
## Apr 2000 0.00000 -0.094410
## May 2000 0.04066 0.009852
## Jun 2000 0.07667 -2.034706
## Jul 2000 -0.01113 -0.133531
muhat.annual <- apply(returns.monthly.x, 2, mean) * 12
## VALE3 PETR3
## 0.2096 0.1584
sigma2.annual <- apply(returns.monthly.x, 2, var) * 12
sigma.annual <- sqrt(sigma2.annual)
## VALE3 PETR3
## 0.5412 0.9223
covmat.annual <- cov(returns.monthly.x) * 12
covhat.annual <- cov(returns.monthly.x)[1, 2] * 12
## [1] 0.07234
rhohat.annual <- cor(returns.monthly.x)[1, 2]
## [1] 0.1449
Para os cálculos da fronteira eficiente vamos separar as variáveis de forma que o sufixo \(i\) é referente a PETR3 e o sufixo \(v\) refere-se a VALE3.
O sufixo \(vi\) relaciona ambas séries temporais.
mu.v = muhat.annual["VALE3"]
mu.i = muhat.annual["PETR3"]
sig2.v = sigma2.annual["VALE3"]
sig2.i = sigma2.annual["PETR3"]
sig.v = sigma.annual["VALE3"]
sig.i = sigma.annual["PETR3"]
sig.vi = covhat.annual
rho.vi = rhohat.annual
Dado o retorno esperado da carteira
\[ \mu_p(x_v, x_i) = x_v \mu_v + x_i \mu_i \]
e a sua variância
\[ \sigma^2_p(x_v, x_i) = \sigma^2_v x_v^2 + \sigma^2_i x_i^2 + 2 x_v x_i \sigma_{vi} \]
vamos calculá-los para diferentes combinações de pesos (\(x_v\) e \(x_i\)) sujeitas a restrição \(x_v + x_i = 1\)
x.v = seq(from = -1, to = 2, by = 0.1) # pesos para VALE3
x.i = 1 - x.v # pesos para PETR3
mu.p = x.v * mu.v + x.i * mu.i # retorno esperado da carteira
sig2.p = sig2.v * x.v^2 + sig2.i * x.i^2 + 2 * x.v * x.i * sig.vi
sig.p = sqrt(sig2.p) # volatilidade da carteira
Destacado em laranja temos os ativos independentes.
Para o cálculo da Sharpe-Ratio da carteira de mínima variância é necessário definir uma taxa livre de risco. Aqui vamos considerar \(r_f = 7\%\).
r.f = 0.07
source("scripts/portfolio.r")
gmin.port = globalMin.portfolio(muhat.annual, covmat.annual)
summary(gmin.port, risk.free = r.f)
## Call:
## globalMin.portfolio(er = muhat.annual, cov.mat = covmat.annual)
##
## Portfolio expected return: 0.1983
## Portfolio standard deviation: 0.4942
## Portfolio Sharpe Ratio: 0.2595
## Portfolio weights:
## VALE3 PETR3
## 0.7792 0.2208
Destacado em azul temos a carteira de mínima variância
Ao considerarmos um ativo livre de risco como mais uma alternativa de investimento chegamos ao seguinte retorno (\(\mu_N\)) da nova carteira que compõe a carteira com 2 ativos mais o ativo livre de risco
\[ \mu_N = r_f + x_p (\mu_p - r_f) \]
tan.port = tangency.portfolio(muhat.annual, covmat.annual, risk.free = r.f)
summary(tan.port, risk.free = r.f)
## Call:
## tangency.portfolio(er = muhat.annual, cov.mat = covmat.annual,
## risk.free = r.f)
##
## Portfolio expected return: 0.2033
## Portfolio standard deviation: 0.5037
## Portfolio Sharpe Ratio: 0.2645
## Portfolio weights:
## VALE3 PETR3
## 0.8767 0.1233
O x marca o ponto em que a linha reta saindo da taxa livre de risco toca a fronteira eficiente e consequentemente indica a carteira tangente que é a carteira eficiente quando se leva em consideração um ativo livre de risco.
Vamos agora calcular a carteira de mínima variância impondo a restrição de não ficar vendido em nenhum ativo (long-only). Dado que para 2 ativos, como visto antes, os ativos caem sobre a fronteira, para produzir uma fronteira eficiente com a restrição de long-only é necessário introduzir pelo menos mais um ativo.
filelist <- c("data/VALE3.monthly.raw.csv", "data/PETR3.monthly.raw.csv",
"data/USIM3.monthly.raw.csv")
returns.monthly.x <- getReturnsFromYahooFiles(filelist)
muhat.annual <- apply(returns.monthly.x, 2, mean) * 12
sigma2.annual <- apply(returns.monthly.x, 2, var) * 12
sigma.annual <- sqrt(sigma2.annual)
covmat.annual <- cov(returns.monthly.x) * 12
covhat.annual <- cov(returns.monthly.x)[1, 2] * 12
rhohat.annual <- cor(returns.monthly.x)[1, 2]
Os problemas de otimização quadrática são descritos como
\[ \min_x \frac{1}{2}\mathbf{x^\prime D x - d^\prime x} \]
Sujeito as restrições
\[ \mathbf{A^{\prime}}_{neq} \mathbf{x} \ge \mathbf{b}_{neq} \]
\[ \mathbf{A^{\prime}}_{eq} \mathbf{x} = \mathbf{b}_{eq} \]
onde condidera-se \(m\) restrições em desigualdades e \(l\) restrições em igualdades. As matrizes tem dimensões \(\mathbf{D} \equiv n\times n\), \(\mathbf{x} \equiv n\times 1\), \(\mathbf{d} \equiv n\times 1\), \(\mathbf{A^{\prime}}_{neq} \equiv m\times n\), \(\mathbf{b}_{neq} \equiv m\times 1\), \(\mathbf{A^{\prime}}_{eq} \equiv l\times n\) e \(\mathbf{b}_{eq} \equiv l\times 1\).
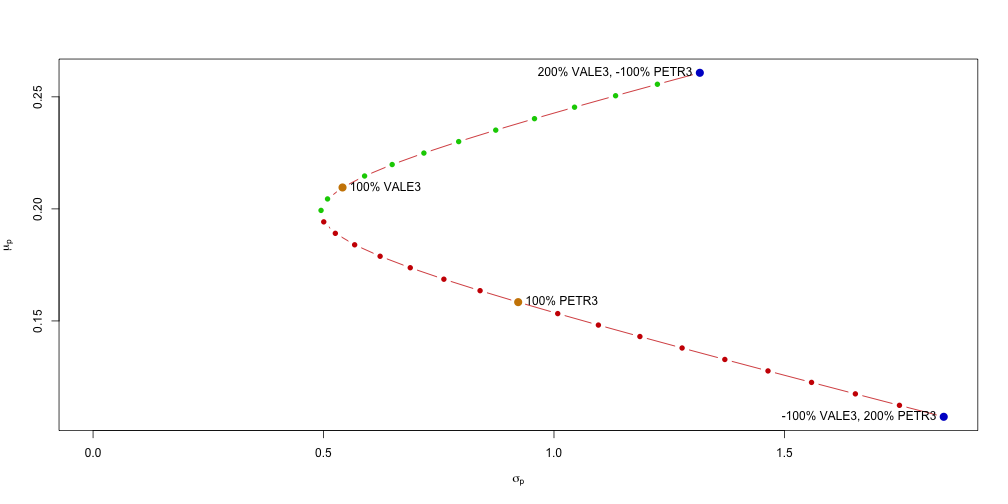
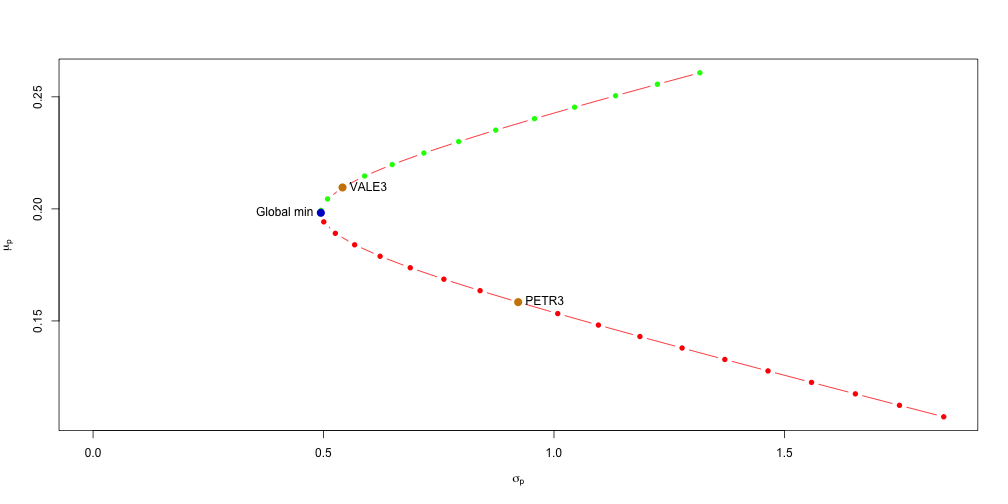
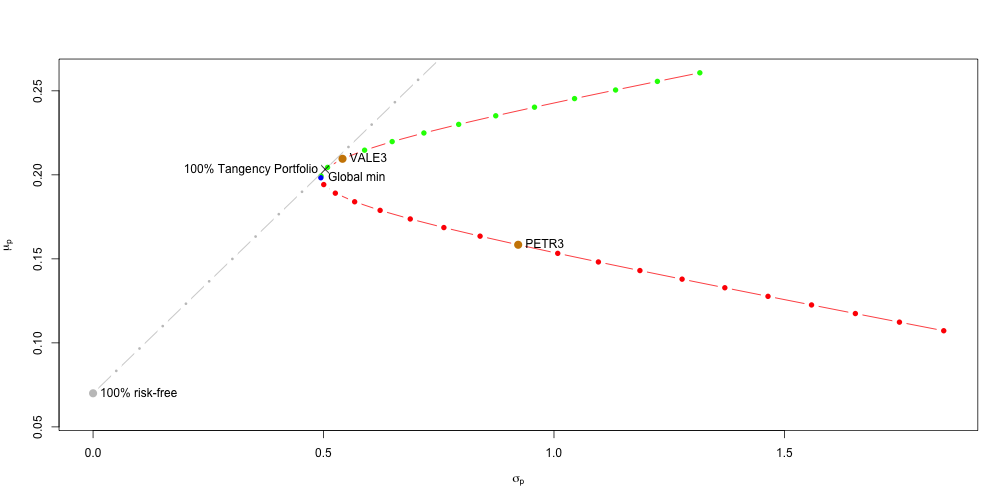
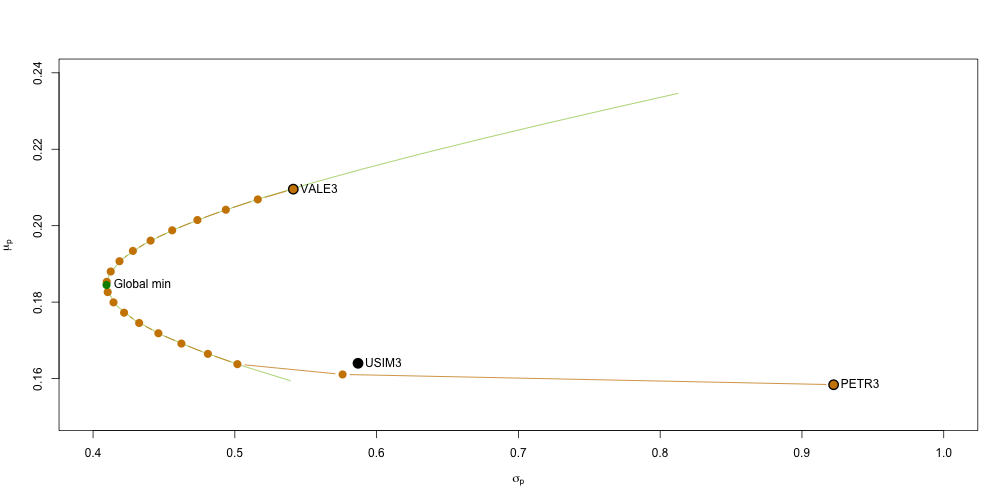
Para colocarmos o problema de otimização de carteiras no framework de otimização quadrática temos que
\[ \mathbf{D} = 2\mathbf{\Sigma}\,\, \mathrm{e} \,\, \mathbf{d} = \mathbf{0} \]
o vetor \(x\) é o vetor de pesos onde \(x_i \ge 0\) para \(i = 1,2,\dots,n\), onde \(n\) é a quantidade de ativos presentes na carteira. Esta restrição representa uma inequação e deve ser especificada com \(l = n\)
\[ \mathbf{A^{\prime}}_{neq} = \mathbf{I}_{n},\, \mathbf{b}_{neq} = \mathbf{0} \]
temos ainda \(m = 1\) restrição em igualdade, onde \(\mathbf{x^{\prime} 1} = 1\) e deve ser especificada como
\[ \mathbf{A^{\prime}}_{eq} = \mathbf{1}^\prime,\, \mathbf{b}_{eq} = 1 \]
O problema pode ainda ser simplificado fazendo
\[ \mathbf{A^{\prime}} = \left( \begin{array}{c} \mathbf{1}^\prime \\ \mathbf{I}_n \end{array} \right),\, \mathbf{b} = \left( \begin{array}{c} 1 \\ \mathbf{0} \end{array} \right) \]
Matriz \(\mathbf{D}\)
D.mat <- 2 * covmat.annual
## VALE3 PETR3 USIM3
## VALE3 0.5858 0.1447 0.1066
## PETR3 0.1447 1.7013 0.0894
## USIM3 0.1066 0.0894 0.6889
Vetor \(\mathbf{d}\)
d.vec <- rep(0, 3)
## [1] 0 0 0
Matriz \(\mathbf{A}\)
A.mat <- cbind(rep(1, 3), diag(3))
## [,1] [,2] [,3] [,4]
## [1,] 1 1 0 0
## [2,] 1 0 1 0
## [3,] 1 0 0 1
Vetor \(\mathbf{b}\)
b.vec <- c(1, rep(0, 3))
## [1] 1 0 0 0
solve.QP para minimizar a variânciaUtilizamos a função solve.QP do pacote quadprog para encontrar a solução do problema de otimização.
library(quadprog)
qp.out <- solve.QP(Dmat = D.mat, dvec = d.vec, Amat = A.mat, bvec = b.vec,
meq = 1)
A solução, que são os pesos dos ativos na carteira ficam no atributo solution da saída da função.
qp.out$solution
## [1] 0.4665 0.1366 0.3969
w.gmin.ns <- qp.out$solution
names(w.gmin.ns) <- names(muhat.annual)
er.gmin.ns <- as.numeric(crossprod(w.gmin.ns, muhat.annual))
var.gmin.ns <- as.numeric(t(w.gmin.ns) %*% covmat.annual %*% w.gmin.ns)
sigma.gmin.ns <- sqrt(var.gmin.ns)
c(er.gmin.ns, sigma.gmin.ns)
## [1] 0.1845 0.4095
A linha verde é a fronteira eficiente long-short e a linha em dourada é a fronteira eficiente long-only.
